
MATH 123 Midterm Notes
linear equations in one variable
consider ax = b where a and b are real numbers
there are then 3 cases:
a ≠ 0: unique solution → x = b/a
a = 0: if b = 0 then any x E R solutions (infinitely many solutions)
a = 0: if b ≠ 0 then the equation 0x = b has no solution
solving systems of linear equations with 2 unknowns
method 1
change one equation to be one variable = to another equation in terms of the other variable
plug into the other equation
solve for the variable
use the variable you’ve solved for to solve for the other variable
e.g.
1) x - y = 3 → x = 3+y plug into 2) for x
2) x + y = 1
plug in:
(3+y) + y = 1
3 + 2y = 1
2y = -2
y = -1
x = 3+y = 3-1 = 2
therefore: x =2, y = -1
method 2 (substraction)
add/subtract the equations should there be a variable that can be cancelled - need variables that cancel each other out
e.g.
1) x - y = 3
2) x + y = 1
add 1) and 2)
x - y = 3
x + y = 1
2x + 0y = 4
2x = 4
x = 1
plug into equation:
x - y = 3
2 - y = 3
y = -1
therefore: x =2, y = -1
row operations
multiply rows by scalars
swap rows
add and subtract rows or multiples of rows
classifying matrices: m x n - rows x columns
sum of 2 matrices
a and b have to be the same size
multiplication of a matrix by a scalar
multiply all entries by the scalar
product of 2 matrices
must have the same inner value (e.g. 2 × 1 • 1 × 3 is defined, 1 × 3 • 2 × 1 is not defined)
matrix multiplication isn’t communitive

let a, b, c be matrices and suppose the operations are defined (rows and columns “agree”) then:
a + b = b + a
a + (b + c) = (a + b) + c
a(bc) = (ab)c
a (b + c) = ab + ac
(b+c)a = ba + ca
a different way to look at systems
x + y = 1
2x - 3y = 5
can be written as
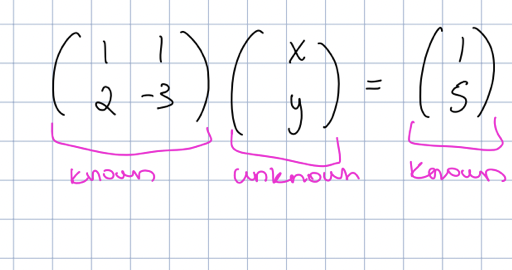


inverses
formula for the inverse of a 2 × 2 matrix
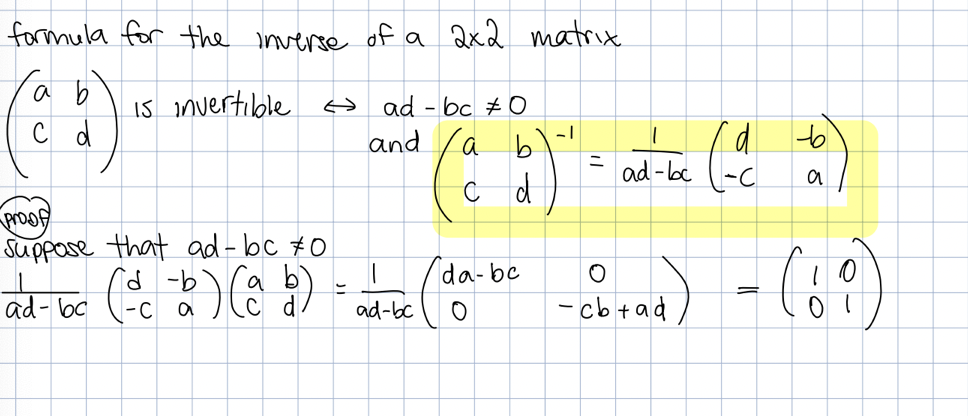
multiplying a matrix by its inverse gives you the identity
let a and b be nxn matrices and suppose ab = Inxn, then ba = Inxn
if a and b are nxn matrices such that ab = Inxn
then b = a⁻¹ and b⁻¹ = a
(a⁻¹)⁻¹ = a
let a and b be invertible nxn matrices then ab is invertible then
(ab)⁻¹ = b⁻¹a⁻¹
let a be an invertible nxn matrix and z ≠ 0 be a real number. then za is invertible and (za)⁻¹ = 1/z a⁻¹
x Inxn = Inxn x = x
linear optimization (graphing to maximize)
maximize the equation
subject to (st)) constraints (inequalities)
set the constraints = (change inequality to =)
find x and y intercepts
draw the lines of the constraints
use a point not on the line to test if statement is true or not while considering inequalities (for the constraints)- if true, shade on the side of that point → use the origin most of the time for simple math
then calculate the points of intersection → from here we can get every corner point of the shaded/allowed region
test corner points by plugging them into the original equation and see what’s the highest/lowest output for max/min
simplex tableau
change the maximize equation to have z in it by making other variables negative and setting to zero (e.g. if x1 + 5x2 + 2x3 = z then change to 0 = -x1 - 5x2 -2x3 + z)
change the constraints by making the inequalities into equal signs and adding slack variables (s) - add a different slack variable to the different constraints; s1, s2…
put this into a table, put the equation with z in the bottom and the =s in like an augmented matrix
choose column with most negative entry in the bottom
take ratios of the end column over the selected column, choose the smaller number as your pivot
make the pivot 1 and clear out the other rows in that column to be zero - do this using regular row operations
keep doing this until you have no negative entries in the bottom
read the table

standard maximum form
a linear program is said to be in standard max form if
the objective function is to be maximized
x1…xn ≥ 0
the constraints of the form a1x1 +…+anxn ≤ b where b≥0
to every problem in standard max form, an initial simplex tableau is associated. solving a linear problem in 2 variables can be done graphically
if the number of variables is ≥3, a graphical solution may be difficult
simplex tableau provides a way of solving linear programs in standard max form
standard minimum form
a linear program is in standard minimum form if
the linear objective function is to be minimized (w = c1,…,cn E R)
all variables are non negative (y1,…, yn ≥ 0)
constraints are of the form a1y1 +a2y2+…+anyn ≥ b with b≥0
a transpose
let a be an mxn matrix At (A transpose) is the matrix obtained by turning the I-th row of A into the I-th column of At → At is an nom matrix
(At)t = A if a is an nxn matrix, and A = At then A is called symmetric

changing from min to max (the dual problem)
without considering slack variables, write data in an augmented matrix
take the transpose of such matrix
rewrite question given new info and use different variables → this is the dual of the original problem
rules for invertibility
no row of zeros on middle
must be square
if 2×2, must not have ad-bc = 0
MATH 123 Midterm Notes
linear equations in one variable
consider ax = b where a and b are real numbers
there are then 3 cases:
a ≠ 0: unique solution → x = b/a
a = 0: if b = 0 then any x E R solutions (infinitely many solutions)
a = 0: if b ≠ 0 then the equation 0x = b has no solution
solving systems of linear equations with 2 unknowns
method 1
change one equation to be one variable = to another equation in terms of the other variable
plug into the other equation
solve for the variable
use the variable you’ve solved for to solve for the other variable
e.g.
1) x - y = 3 → x = 3+y plug into 2) for x
2) x + y = 1
plug in:
(3+y) + y = 1
3 + 2y = 1
2y = -2
y = -1
x = 3+y = 3-1 = 2
therefore: x =2, y = -1
method 2 (substraction)
add/subtract the equations should there be a variable that can be cancelled - need variables that cancel each other out
e.g.
1) x - y = 3
2) x + y = 1
add 1) and 2)
x - y = 3
x + y = 1
2x + 0y = 4
2x = 4
x = 1
plug into equation:
x - y = 3
2 - y = 3
y = -1
therefore: x =2, y = -1
row operations
multiply rows by scalars
swap rows
add and subtract rows or multiples of rows
classifying matrices: m x n - rows x columns
sum of 2 matrices
a and b have to be the same size
multiplication of a matrix by a scalar
multiply all entries by the scalar
product of 2 matrices
must have the same inner value (e.g. 2 × 1 • 1 × 3 is defined, 1 × 3 • 2 × 1 is not defined)
matrix multiplication isn’t communitive

let a, b, c be matrices and suppose the operations are defined (rows and columns “agree”) then:
a + b = b + a
a + (b + c) = (a + b) + c
a(bc) = (ab)c
a (b + c) = ab + ac
(b+c)a = ba + ca
a different way to look at systems
x + y = 1
2x - 3y = 5
can be written as



inverses
formula for the inverse of a 2 × 2 matrix
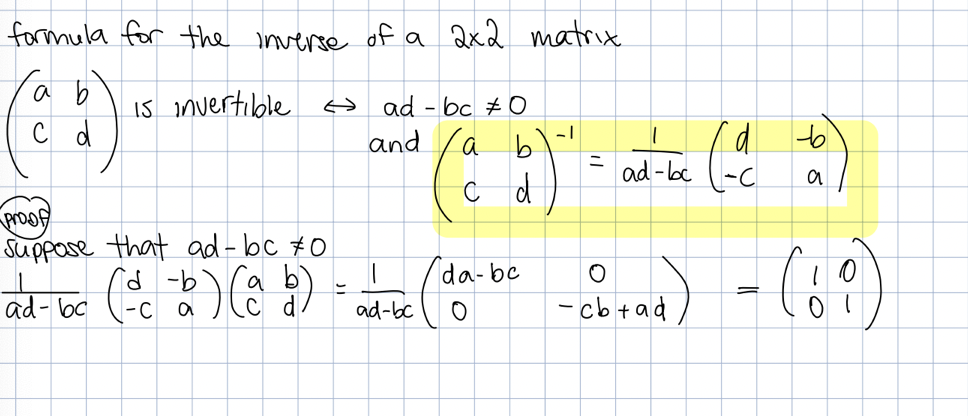
multiplying a matrix by its inverse gives you the identity
let a and b be nxn matrices and suppose ab = Inxn, then ba = Inxn
if a and b are nxn matrices such that ab = Inxn
then b = a⁻¹ and b⁻¹ = a
(a⁻¹)⁻¹ = a
let a and b be invertible nxn matrices then ab is invertible then
(ab)⁻¹ = b⁻¹a⁻¹
let a be an invertible nxn matrix and z ≠ 0 be a real number. then za is invertible and (za)⁻¹ = 1/z a⁻¹
x Inxn = Inxn x = x
linear optimization (graphing to maximize)
maximize the equation
subject to (st)) constraints (inequalities)
set the constraints = (change inequality to =)
find x and y intercepts
draw the lines of the constraints
use a point not on the line to test if statement is true or not while considering inequalities (for the constraints)- if true, shade on the side of that point → use the origin most of the time for simple math
then calculate the points of intersection → from here we can get every corner point of the shaded/allowed region
test corner points by plugging them into the original equation and see what’s the highest/lowest output for max/min
simplex tableau
change the maximize equation to have z in it by making other variables negative and setting to zero (e.g. if x1 + 5x2 + 2x3 = z then change to 0 = -x1 - 5x2 -2x3 + z)
change the constraints by making the inequalities into equal signs and adding slack variables (s) - add a different slack variable to the different constraints; s1, s2…
put this into a table, put the equation with z in the bottom and the =s in like an augmented matrix
choose column with most negative entry in the bottom
take ratios of the end column over the selected column, choose the smaller number as your pivot
make the pivot 1 and clear out the other rows in that column to be zero - do this using regular row operations
keep doing this until you have no negative entries in the bottom
read the table

standard maximum form
a linear program is said to be in standard max form if
the objective function is to be maximized
x1…xn ≥ 0
the constraints of the form a1x1 +…+anxn ≤ b where b≥0
to every problem in standard max form, an initial simplex tableau is associated. solving a linear problem in 2 variables can be done graphically
if the number of variables is ≥3, a graphical solution may be difficult
simplex tableau provides a way of solving linear programs in standard max form
standard minimum form
a linear program is in standard minimum form if
the linear objective function is to be minimized (w = c1,…,cn E R)
all variables are non negative (y1,…, yn ≥ 0)
constraints are of the form a1y1 +a2y2+…+anyn ≥ b with b≥0
a transpose
let a be an mxn matrix At (A transpose) is the matrix obtained by turning the I-th row of A into the I-th column of At → At is an nom matrix
(At)t = A if a is an nxn matrix, and A = At then A is called symmetric

changing from min to max (the dual problem)
without considering slack variables, write data in an augmented matrix
take the transpose of such matrix
rewrite question given new info and use different variables → this is the dual of the original problem
rules for invertibility
no row of zeros on middle
must be square
if 2×2, must not have ad-bc = 0
 Knowt
Knowt