
Unit 8: Applications of Integration
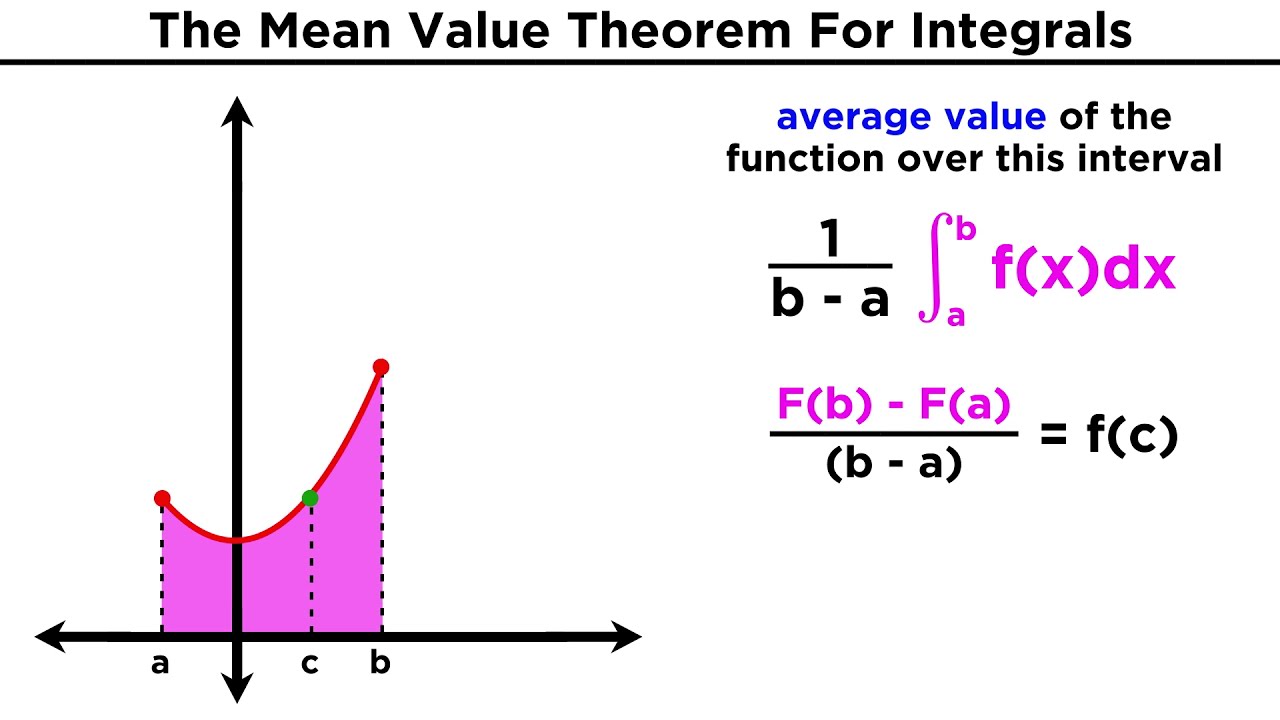
Average Value of Functions
Remember that to calculate the average we add everything up and then divide!
The integral is the summation of everything, so we can use it to find the average of a function!
The only thing we have to change is by dividing our integral!
For example, if we had the interval 0 to 40, we can take the integral of our function and divide it by our interval! So it would be 1/40 * ∫f(x)
Position, Velocity, and Acceleration
Similar to how we can go from position → velocity using the derivative, we can do the reverse using the integral!
Displacement | ∫v(t) |
|---|---|
Position | ∫|v(t)|(Absolute value) |
Velocity | ∫a(t) |
Remember that the FTC still applies, for example velocity will be equal to ∫a(t) from a to b which is: ∫a(t) = v(b) - v(a)
Area Between Two Curves
The integral gives us the area below a function
Therefore, we can subtract the area of one function and another to get the area between the two!
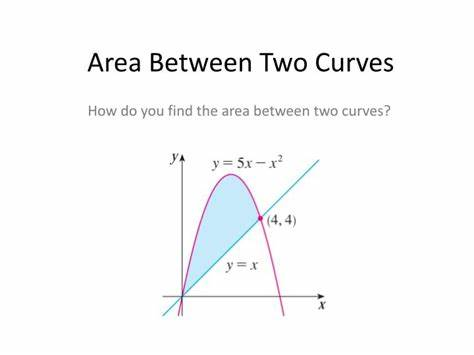
Finding this area is pretty simple, all we have to do is integrate the top function & subtract the bottom function!
We need to take the integral from where the functions start (normally zero) to where they intersect
For the problem we would have ∫5x-x^2 from 0 to 4 - ∫x from 0 to 4
Most all problems for area between two curves will be similar to this
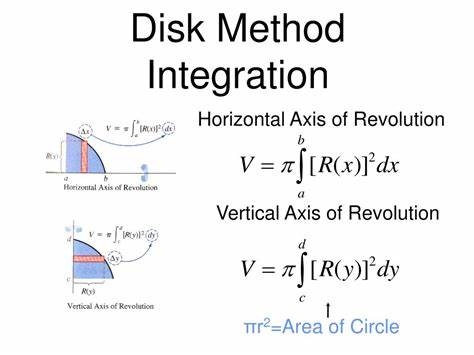
Volume by Cross Sectional Area
We get a 2D shape from the area under a curve, if we rotate this shape → we get a 3D object
To find the area we just integrate the volume formula!
What is the formula for finding the volume of a shape using integrals?
To find the volume of a shape using integrals, we use the formula for the cross-sectional area (length times width) and multiply it by the height, which is represented by the variable "dx" in the integral. Therefore, the formula for the volume of a rectangular shape using integrals is:
V = ∫(length x width) dx
where V is the volume, and the integral is taken over the range of the height of the shape.
That would give us the volume for a rectangle (because their area is just l * w)
The majority of the time, when we are integrating a curve, we get discs or circles
Therefore, we can almost always use the disc method to find our volume
We know that the area of a circle is πr^2
So using our integral we would have V = ∫πr^2
You can combine this with area between two curves problems and have ∫πR^2 - ∫πr^2]
Unit 8: Applications of Integration
Average Value of Functions
Remember that to calculate the average we add everything up and then divide!
The integral is the summation of everything, so we can use it to find the average of a function!
The only thing we have to change is by dividing our integral!
For example, if we had the interval 0 to 40, we can take the integral of our function and divide it by our interval! So it would be 1/40 * ∫f(x)

Position, Velocity, and Acceleration
Similar to how we can go from position → velocity using the derivative, we can do the reverse using the integral!
Displacement | ∫v(t) |
|---|---|
Position | ∫|v(t)|(Absolute value) |
Velocity | ∫a(t) |
Remember that the FTC still applies, for example velocity will be equal to ∫a(t) from a to b which is: ∫a(t) = v(b) - v(a)
Area Between Two Curves
The integral gives us the area below a function
Therefore, we can subtract the area of one function and another to get the area between the two!

Finding this area is pretty simple, all we have to do is integrate the top function & subtract the bottom function!
We need to take the integral from where the functions start (normally zero) to where they intersect
For the problem we would have ∫5x-x^2 from 0 to 4 - ∫x from 0 to 4
Most all problems for area between two curves will be similar to this
Volume by Cross Sectional Area
We get a 2D shape from the area under a curve, if we rotate this shape → we get a 3D object
To find the area we just integrate the volume formula!
What is the formula for finding the volume of a shape using integrals?
To find the volume of a shape using integrals, we use the formula for the cross-sectional area (length times width) and multiply it by the height, which is represented by the variable "dx" in the integral. Therefore, the formula for the volume of a rectangular shape using integrals is:
V = ∫(length x width) dx
where V is the volume, and the integral is taken over the range of the height of the shape.
That would give us the volume for a rectangle (because their area is just l * w)
The majority of the time, when we are integrating a curve, we get discs or circles
Therefore, we can almost always use the disc method to find our volume
We know that the area of a circle is πr^2
So using our integral we would have V = ∫πr^2
You can combine this with area between two curves problems and have ∫πR^2 - ∫πr^2]

 Knowt
Knowt