
Unit 1: Limits and Continuity
Limits
Limits are the value that a function approaches as the variable within the function gets nearer to a particular value.
We don’t really care what’s happening at the point, we care about what’s happening around the point
To find the limit of a simple polynomial, plug in the number that the variable is approaching
Ways to Find Limits
Look on a graph to see what it approaches
If the graph approaches two different values for the same number, the limit does not exist
Estimate from a table
Algebraic Properties
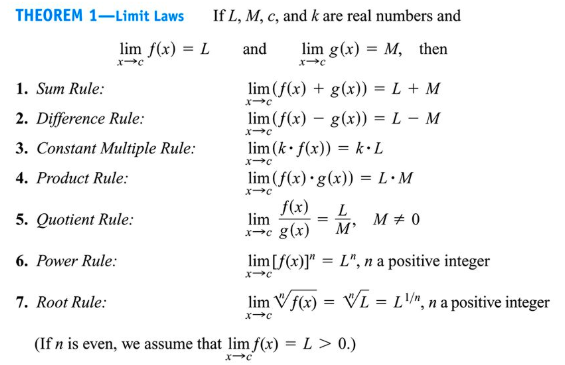
Algebraic Manipulation
You can factor the numerator and denominator, then cancel any removable discontinuities
This is mostly useful if you get limits where the denominator is equal to 0
For example, (x+3)(x+2)/(x+3)(x-3)
(x+3) is able to be removed → removable discontinuity
Squeeze Theorem
Conditions
For all values of x in the interval that contains a, g(x) ≤ f(x) ≤ h(x)
g and h have the same limit as x approaches a
lim g(x) = L, lim h(x) = L, therefore lim f(x) = L
Trig limits as x approaches 0:
lim [sin(x)/x] = 1
lim [(cos(x)-1)/x] = 0
lim [sin(ax)/x] = a
lim [sin(ax)/sin(bx)] = a/b
Continuity
Jump Discontinuity
Occurs when the curve “breaks” at a particular place and starts somewhere else
The limits from the left and the right will both exist, but they will not match
Essential/Infinite Discontinuity
The curve has a vertical asymptote
Removable Discontinuity
An otherwise continuous curve has a hole in it
“Removable” because one can remove the discontinuity by filling the hole
Continuity Conditions
For f(x) to be continuous when x=c:
f(c) exists
the limit as x→c exists
lim f(x) = f(c)
x→c
A function is continuous on an interval if it is continuous at every point on that interval
Removing Discontinuities
You can remove a discontinuity by redefining the function without that point in the domain
This is frequently done by factoring out a common root between the numerator and denominator
Limits and Asymptotes
Vertical asymptote: a line that a function cannot cross because the function is undefined there
Horizontal asymptote: the end behavior of a function
A horizontal asymptote can be crossed
Horizontal Asymptote Rules
If the highest power of x in a rational expression is in the numerator, then the limit as x approaches infinity is infinity: there is no horizontal asymptote
If the highest power of x is in the denominator, then the limit as x approaches infinity is zero and the horizontal asymptote is the line y=0
If the highest power is the same, then the limit is the coefficient of the highest term in the numerator divided by the coefficient of the highest term in the denominator
Intermediate Value Theorem (IVT)
IVT - Guarantees that if a function f(x) is continuous on the interval [a,b] and C is any number between f(a) and f(b), ten there is at least one number in the interval [a,b] such that f(x) = C
Unit 1: Limits and Continuity
Limits
Limits are the value that a function approaches as the variable within the function gets nearer to a particular value.
We don’t really care what’s happening at the point, we care about what’s happening around the point
To find the limit of a simple polynomial, plug in the number that the variable is approaching
Ways to Find Limits
Look on a graph to see what it approaches
If the graph approaches two different values for the same number, the limit does not exist
Estimate from a table
Algebraic Properties
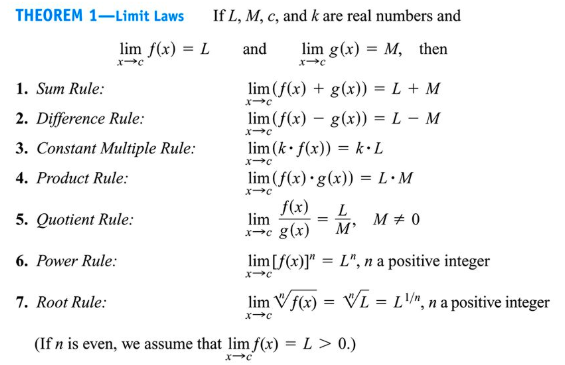
Algebraic Manipulation
You can factor the numerator and denominator, then cancel any removable discontinuities
This is mostly useful if you get limits where the denominator is equal to 0
For example, (x+3)(x+2)/(x+3)(x-3)
(x+3) is able to be removed → removable discontinuity
Squeeze Theorem
Conditions
For all values of x in the interval that contains a, g(x) ≤ f(x) ≤ h(x)
g and h have the same limit as x approaches a
lim g(x) = L, lim h(x) = L, therefore lim f(x) = L
Trig limits as x approaches 0:
lim [sin(x)/x] = 1
lim [(cos(x)-1)/x] = 0
lim [sin(ax)/x] = a
lim [sin(ax)/sin(bx)] = a/b
Continuity
Jump Discontinuity
Occurs when the curve “breaks” at a particular place and starts somewhere else
The limits from the left and the right will both exist, but they will not match
Essential/Infinite Discontinuity
The curve has a vertical asymptote
Removable Discontinuity
An otherwise continuous curve has a hole in it
“Removable” because one can remove the discontinuity by filling the hole
Continuity Conditions
For f(x) to be continuous when x=c:
f(c) exists
the limit as x→c exists
lim f(x) = f(c)
x→c
A function is continuous on an interval if it is continuous at every point on that interval
Removing Discontinuities
You can remove a discontinuity by redefining the function without that point in the domain
This is frequently done by factoring out a common root between the numerator and denominator
Limits and Asymptotes
Vertical asymptote: a line that a function cannot cross because the function is undefined there
Horizontal asymptote: the end behavior of a function
A horizontal asymptote can be crossed
Horizontal Asymptote Rules
If the highest power of x in a rational expression is in the numerator, then the limit as x approaches infinity is infinity: there is no horizontal asymptote
If the highest power of x is in the denominator, then the limit as x approaches infinity is zero and the horizontal asymptote is the line y=0
If the highest power is the same, then the limit is the coefficient of the highest term in the numerator divided by the coefficient of the highest term in the denominator
Intermediate Value Theorem (IVT)
IVT - Guarantees that if a function f(x) is continuous on the interval [a,b] and C is any number between f(a) and f(b), ten there is at least one number in the interval [a,b] such that f(x) = C
 Knowt
Knowt