
Math 119: Mathematics for Elementary School Teachers
this shouldn’t be used as a substitute for going to class btw :p
Polya’s Problem Solving Four Steps
Understanding the Problem
Devising a Plan
Carrying Out the Plan
Looking Back
Five Problem-Solving Strategies
Making a Drawing
Guessing and Checking
Making a Table
Finding a Pattern
Geometric Sequence
Each new number is obtained by multiplying the previous number by a common ratio
a) 5, 25, 125… Next term: (625), The type of sequence: geometric
the common ratio here is 5
5 x 5 = 25, 25 x 5 = 125, etc.
b) 1, 6, 36, 216… Next term: (1296), The type of sequence: geometric
the common ratio here is 6
1 x 6 = 6, 6 x 6 = 36, 36 x 6 = 216, etc.
Arithmetic Sequence
Each new number is obtained from the previous number in the sequence by adding a common difference
a) 5, 10, 15… Next term: (20), The type of sequence: arithmetic
the common difference here is 5
5 + 5 = 10, 10 + 5 = 15, 15 + 5 = 20
b) 9, 18, 27… Next term: (36), The type of sequence: arithmetic
the common difference here is 9
9 + 9 = 18, 18 + 9 = 27, 27 + 9 = 36
Finite Differences
A method approaching number patterns can be found by looking at the differences between consecutive terms
a) 0, 3, 8, 15, 24
the difference between each number increases by 2
3 - 0 = 3, 8 - 3 = 5, 15 - 8 = 7, 24 - 15 = 9
using this, we can find the next number in the chain
9 + 2 = 11, 24 + 11 = 35, so the next number is 35
b) 1, 4, 9, 16, 25
the difference between each number increases by 2
4 - 1 = 3, 9 - 4 = 5, 16 - 9 = 7, 25 - 16 = 9
using this, we can find the next number in the chain
add two to nine, 9 + 2 = 11, then add the sum to the last number in the sequence (25), 25 + 11 = 36
Fibonacci Numbers
After the first two sequence of numbers, each successive number can be obtained by adding the previous two numbers
a) 1, 1, 2, 3, 5, 8… The next term is (?)
add the first two numbers, 1 + 1= 2, then the sum by the previous number, 2 + 1 = 3, and continue
3 + 2 = 5, 5 + 3 = 8, 8 + 5 = 13
therefore, our next term is 13
Inductive Reasoning
The process of forming conclusions on the basis of patterns and observations, also called an informed guess
a) Mary has two eyes
Max has two eyes
Mason has two eyes
Mary, Max and Mason are human beings
Therefore, human beings have two eyes.
the pattern here is that all the people have two eyes, and since they are all humans, it can be inferred that all humans have two eyes
b) 1 + 2 + 3 = 6
2 + 3 + 4 = 9
3 + 4 + 5 = 12
4 + 5 + 6 = ?
the pattern here is that each sum increasing by 3
therefore, we can infer that the final sum will also increase by 3
12 + 3 = 15
we should check our answer, though, just to make sure it’s correct
4 + 5 = 9, 9 + 6 = 15
Deductive Reasoning
The process of forming conclusions on the basis of logic, or reasoning from one or more statements to reach a logical conclusion
Has three components
Logic is the science that evaluates the argument, which is a group of statements including one or more premises and one and only one conclusion (or a statement that is either true or false)
Premise is a statement that provides reason or support for the conclusion
Conclusion is a statement in an argument that convinces the audience
a) Given Statements (or Premises)
The sum of two numbers is 24
One of the numbers is 10
Given this information, we can subtract 10 from 24 and find the conclusion
24 - 10 = 14
Conclusion
The other number is 14.
Venn Diagrams and Deductive Reasoning
Venn diagrams are used to representing information, and using deductive reasoning with these diagrams can help us draw conclusions
a) Premises
All students in room 210 are taking English 441
All students who are taking English 441 are students at Queens College
Conclusion
Therefore, all students in room 210 are students at Queens College
now, to represent this in a diagram
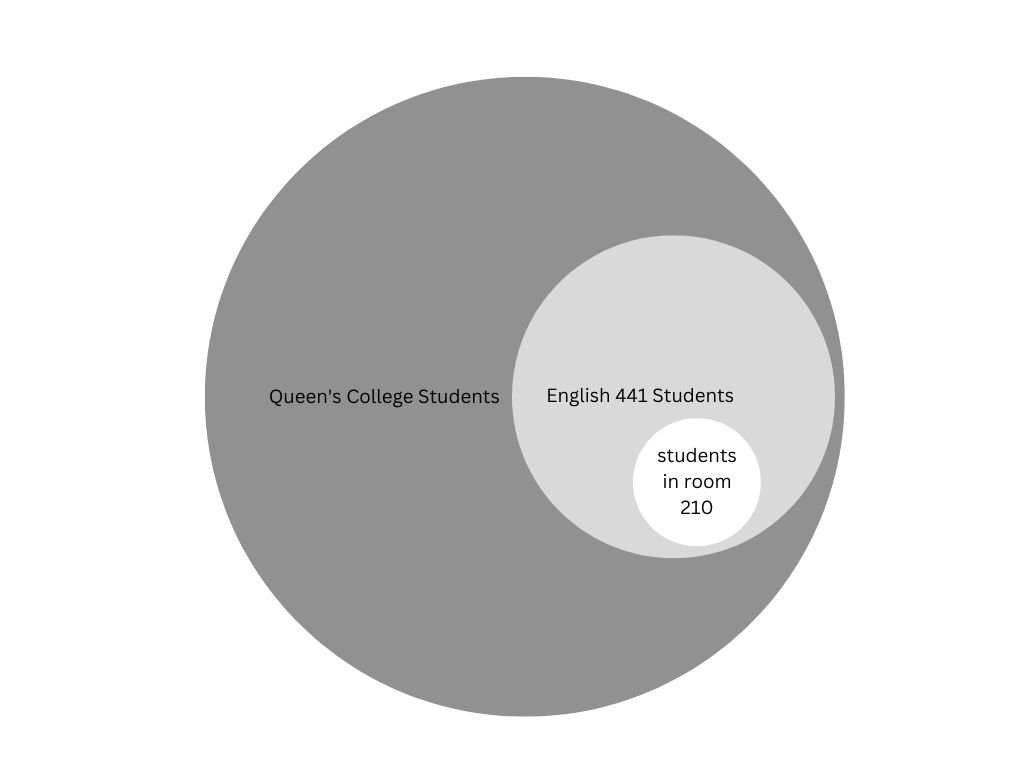 b) Premises
b) Premises
All orcas are whales
All whales are mammals
Conclusion
All orcas are mammals
 Law of Detachment
Law of Detachment
When a conditional statement is given (premise 1), and the if part is satisfied (premise 2), the then part will logically follow
Premises
If p, then q
p
Conclusion
q (valid)
a) Premises
If the temperature is below 32F, then water will freeze.
The temperature is below 32F today.
Conclusion
Water will freeze.
b) Premises
If the trip is over 300 miles, the campers will run out of fuel.
The campers ran out of fuel.
Conclusion
The trip was over 300 miles.
Law of Contraposition
When a conditional statement is given (premise 1) and the negation of the then part is given (premise 2), the negation of the if part will logically follow
Premises
If p, then q
Not q
Conclusion
Not p (valid)
a) Premises
If the temperature is below 32F, then water will freeze.
The temperature is not below 32F today.
Conclusion
Water will not freeze.
b) Premises
If the trip is over 300 miles, the campers will run out of fuel.
The campers did not run out of fuel.
Conclusion
The trip was not over 300 miles.
Conditional Statement Forms
Conditional Statement
If p, then q.
If a person lives in NY, then the person lives in the United States
Converse
If q, then p.
If a person lives in the United States, then the person lives in NY
the converse is not always true
Inverse
If not p, the not q.
If the person does not live in NY, then they do not live in the United States
the inverse is not always true
Contrapositive
If not q, then not p.
If the person does not live in the United States, then they do not live in NY
the contrapositive is not always true
a) “Someone lives in NY in the United States”
Conditional: If someone lives in NY, then the person lives in the United States
Converse: If a person lives in the United States, then the person lives in NY
Inverse: If the person does not live in NY, then they do not live in the United States
Contrapositive: If the person does not live in the United States, then they do not live in NY
Venn Diagram for Conditional Statements
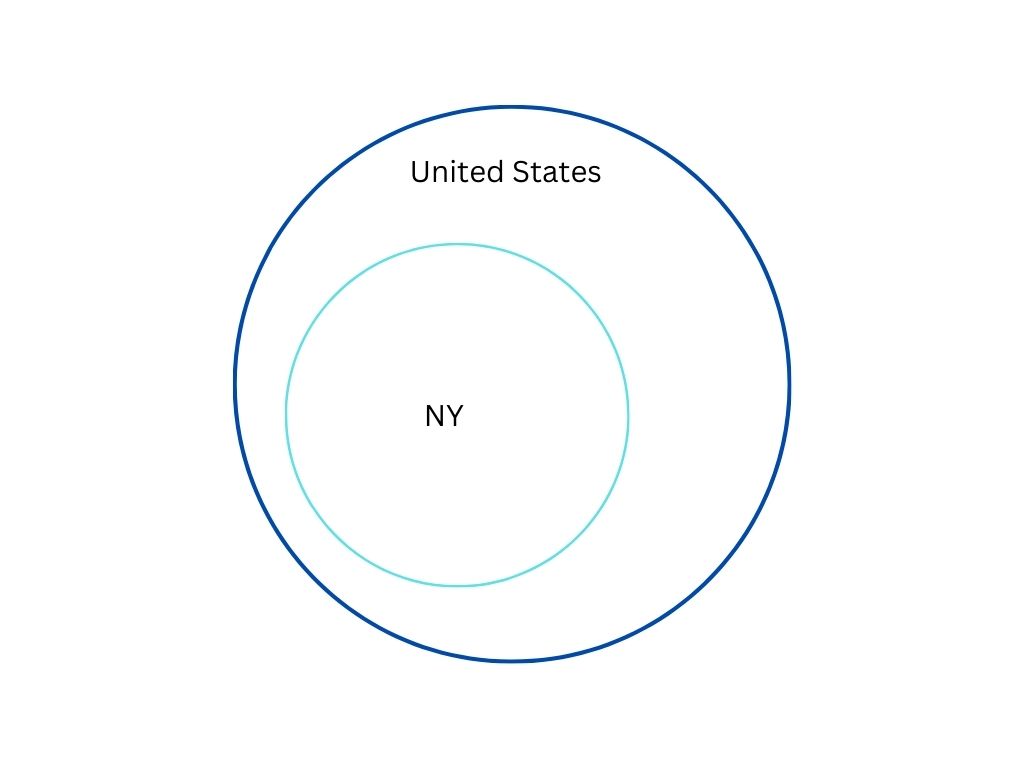 Sets
Sets
A collection of objects called “elements”
There are two common methods of specifying a set;
describing the elements of the set with words (“positive integers less than 5”)
listing the elements of the set between set braces, {}
When Listing Elements
No repetition: the elements of a set are listed without repetition
{1, 2, 2, 3} - incorrect
{1, 2, 3} - correct
Ellipsis: if the set of elements is large, begin the list and then use three dots
“Positive integers less than 100” are listed as {1, 2, 3, 4 … }
Empty set (Null set): if a set has no elements, the set is called the empty set and is denoted by {} or a circle with a diagonal line through it
Naming Sets and Set Elements
Denotation
Naming sets - uppercase letters (A, B, S)
Denoting elements of sets - lowercase letters (a, b, s)
E.x., A = {a, b, c…}
Symbol
E: an element of a set
b is an element of set A, so b E A
Math 119: Mathematics for Elementary School Teachers
this shouldn’t be used as a substitute for going to class btw :p
Polya’s Problem Solving Four Steps
Understanding the Problem
Devising a Plan
Carrying Out the Plan
Looking Back
Five Problem-Solving Strategies
Making a Drawing
Guessing and Checking
Making a Table
Finding a Pattern
Geometric Sequence
Each new number is obtained by multiplying the previous number by a common ratio
a) 5, 25, 125… Next term: (625), The type of sequence: geometric
the common ratio here is 5
5 x 5 = 25, 25 x 5 = 125, etc.
b) 1, 6, 36, 216… Next term: (1296), The type of sequence: geometric
the common ratio here is 6
1 x 6 = 6, 6 x 6 = 36, 36 x 6 = 216, etc.
Arithmetic Sequence
Each new number is obtained from the previous number in the sequence by adding a common difference
a) 5, 10, 15… Next term: (20), The type of sequence: arithmetic
the common difference here is 5
5 + 5 = 10, 10 + 5 = 15, 15 + 5 = 20
b) 9, 18, 27… Next term: (36), The type of sequence: arithmetic
the common difference here is 9
9 + 9 = 18, 18 + 9 = 27, 27 + 9 = 36
Finite Differences
A method approaching number patterns can be found by looking at the differences between consecutive terms
a) 0, 3, 8, 15, 24
the difference between each number increases by 2
3 - 0 = 3, 8 - 3 = 5, 15 - 8 = 7, 24 - 15 = 9
using this, we can find the next number in the chain
9 + 2 = 11, 24 + 11 = 35, so the next number is 35
b) 1, 4, 9, 16, 25
the difference between each number increases by 2
4 - 1 = 3, 9 - 4 = 5, 16 - 9 = 7, 25 - 16 = 9
using this, we can find the next number in the chain
add two to nine, 9 + 2 = 11, then add the sum to the last number in the sequence (25), 25 + 11 = 36
Fibonacci Numbers
After the first two sequence of numbers, each successive number can be obtained by adding the previous two numbers
a) 1, 1, 2, 3, 5, 8… The next term is (?)
add the first two numbers, 1 + 1= 2, then the sum by the previous number, 2 + 1 = 3, and continue
3 + 2 = 5, 5 + 3 = 8, 8 + 5 = 13
therefore, our next term is 13
Inductive Reasoning
The process of forming conclusions on the basis of patterns and observations, also called an informed guess
a) Mary has two eyes
Max has two eyes
Mason has two eyes
Mary, Max and Mason are human beings
Therefore, human beings have two eyes.
the pattern here is that all the people have two eyes, and since they are all humans, it can be inferred that all humans have two eyes
b) 1 + 2 + 3 = 6
2 + 3 + 4 = 9
3 + 4 + 5 = 12
4 + 5 + 6 = ?
the pattern here is that each sum increasing by 3
therefore, we can infer that the final sum will also increase by 3
12 + 3 = 15
we should check our answer, though, just to make sure it’s correct
4 + 5 = 9, 9 + 6 = 15
Deductive Reasoning
The process of forming conclusions on the basis of logic, or reasoning from one or more statements to reach a logical conclusion
Has three components
Logic is the science that evaluates the argument, which is a group of statements including one or more premises and one and only one conclusion (or a statement that is either true or false)
Premise is a statement that provides reason or support for the conclusion
Conclusion is a statement in an argument that convinces the audience
a) Given Statements (or Premises)
The sum of two numbers is 24
One of the numbers is 10
Given this information, we can subtract 10 from 24 and find the conclusion
24 - 10 = 14
Conclusion
The other number is 14.
Venn Diagrams and Deductive Reasoning
Venn diagrams are used to representing information, and using deductive reasoning with these diagrams can help us draw conclusions
a) Premises
All students in room 210 are taking English 441
All students who are taking English 441 are students at Queens College
Conclusion
Therefore, all students in room 210 are students at Queens College
now, to represent this in a diagram
 b) Premises
b) Premises
All orcas are whales
All whales are mammals
Conclusion
All orcas are mammals
 Law of Detachment
Law of Detachment
When a conditional statement is given (premise 1), and the if part is satisfied (premise 2), the then part will logically follow
Premises
If p, then q
p
Conclusion
q (valid)
a) Premises
If the temperature is below 32F, then water will freeze.
The temperature is below 32F today.
Conclusion
Water will freeze.
b) Premises
If the trip is over 300 miles, the campers will run out of fuel.
The campers ran out of fuel.
Conclusion
The trip was over 300 miles.
Law of Contraposition
When a conditional statement is given (premise 1) and the negation of the then part is given (premise 2), the negation of the if part will logically follow
Premises
If p, then q
Not q
Conclusion
Not p (valid)
a) Premises
If the temperature is below 32F, then water will freeze.
The temperature is not below 32F today.
Conclusion
Water will not freeze.
b) Premises
If the trip is over 300 miles, the campers will run out of fuel.
The campers did not run out of fuel.
Conclusion
The trip was not over 300 miles.
Conditional Statement Forms
Conditional Statement
If p, then q.
If a person lives in NY, then the person lives in the United States
Converse
If q, then p.
If a person lives in the United States, then the person lives in NY
the converse is not always true
Inverse
If not p, the not q.
If the person does not live in NY, then they do not live in the United States
the inverse is not always true
Contrapositive
If not q, then not p.
If the person does not live in the United States, then they do not live in NY
the contrapositive is not always true
a) “Someone lives in NY in the United States”
Conditional: If someone lives in NY, then the person lives in the United States
Converse: If a person lives in the United States, then the person lives in NY
Inverse: If the person does not live in NY, then they do not live in the United States
Contrapositive: If the person does not live in the United States, then they do not live in NY
Venn Diagram for Conditional Statements
 Sets
Sets
A collection of objects called “elements”
There are two common methods of specifying a set;
describing the elements of the set with words (“positive integers less than 5”)
listing the elements of the set between set braces, {}
When Listing Elements
No repetition: the elements of a set are listed without repetition
{1, 2, 2, 3} - incorrect
{1, 2, 3} - correct
Ellipsis: if the set of elements is large, begin the list and then use three dots
“Positive integers less than 100” are listed as {1, 2, 3, 4 … }
Empty set (Null set): if a set has no elements, the set is called the empty set and is denoted by {} or a circle with a diagonal line through it
Naming Sets and Set Elements
Denotation
Naming sets - uppercase letters (A, B, S)
Denoting elements of sets - lowercase letters (a, b, s)
E.x., A = {a, b, c…}
Symbol
E: an element of a set
b is an element of set A, so b E A
 Knowt
Knowt