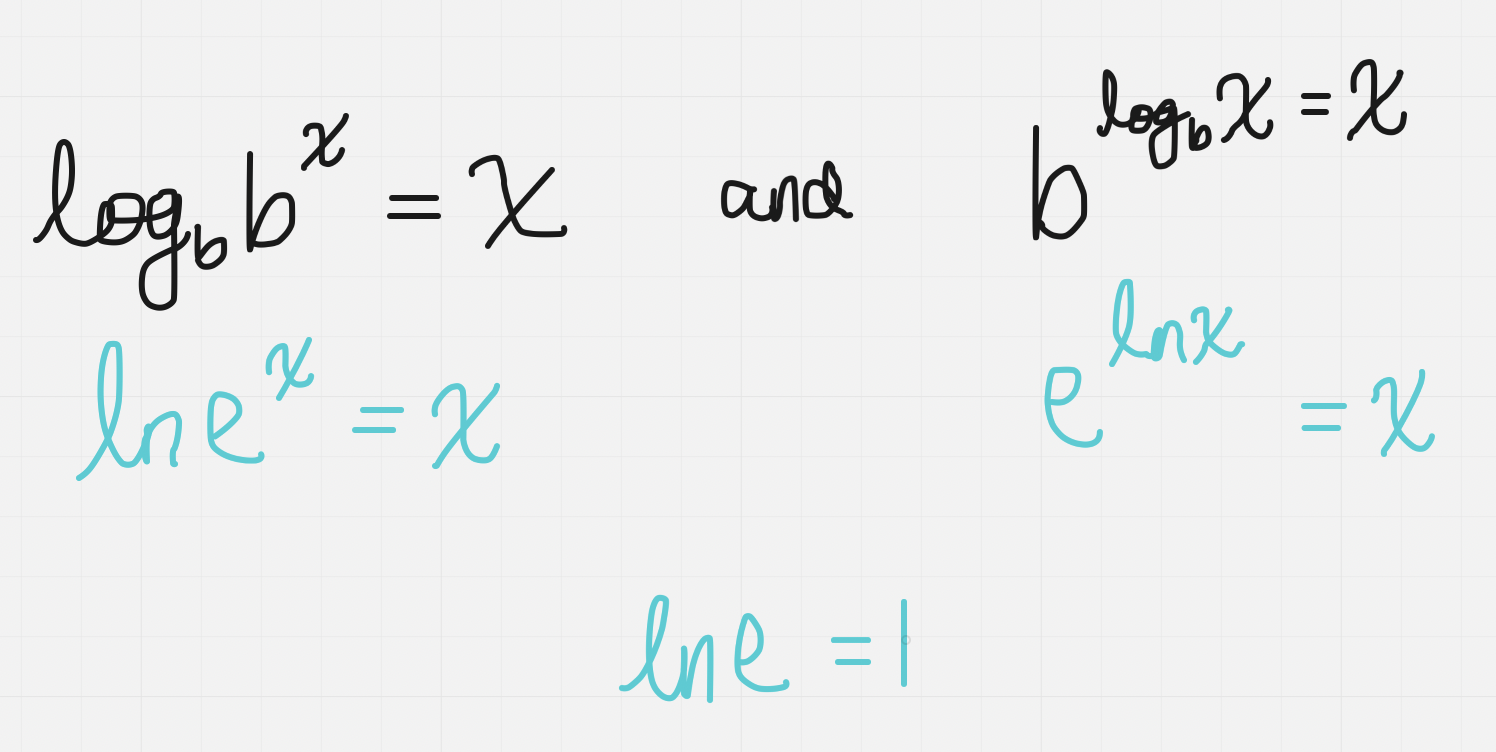12-05: Special Derivatives (Sinusoidal and Exponential Functions)
IROC of Sinusoidal Functions
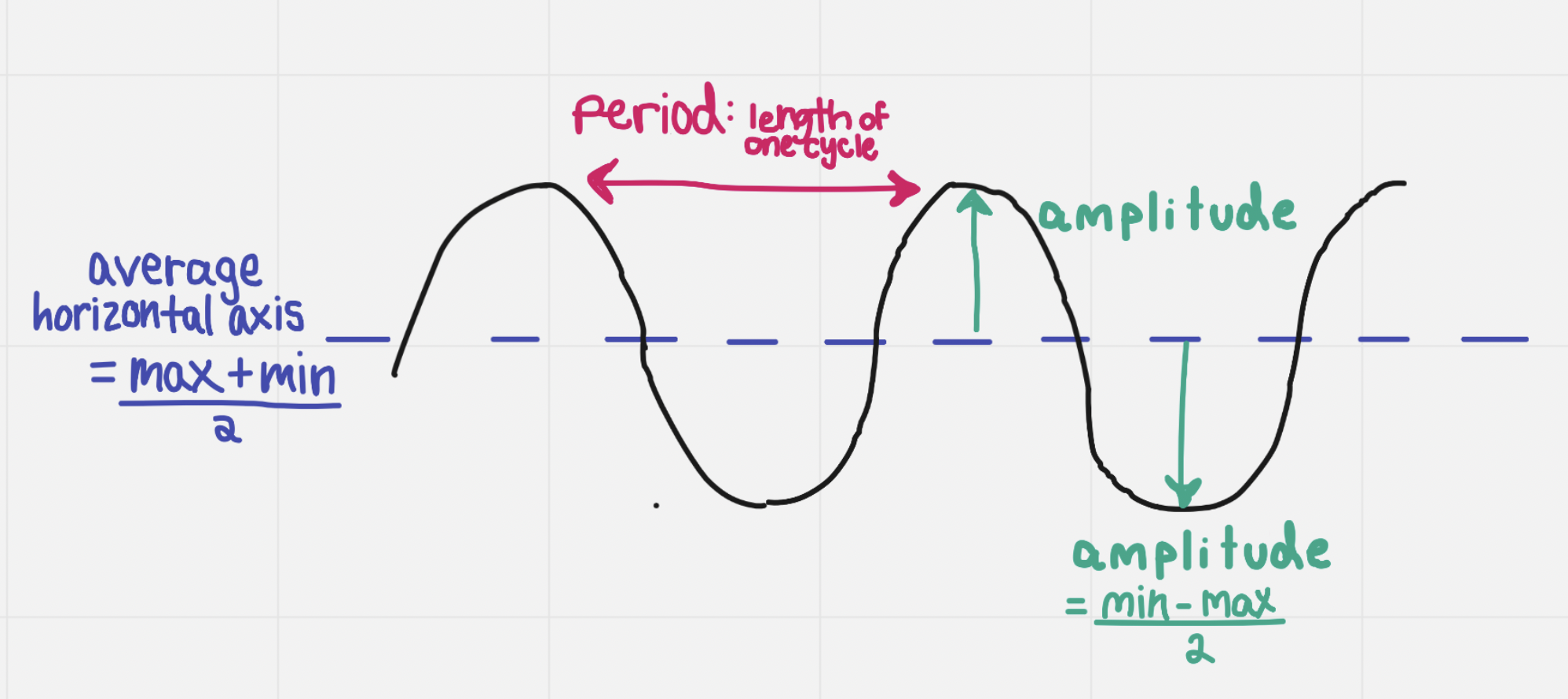
Sinusoidal function: functions where graphs have the same shape as a sine wave
Properties of sinusoidal functions:
y=sinx and its derivative
Derivative of y=sinx is y=cosx
This is because the slope of the tangent line gets “derivative-d” and then becomes a point
In the original, mtangent=1 when increasing, this becomes the new y value
→ Otherwise, consider the points where mtangent=0, these become intercepts as we learned before where min and max points become intercepts when deriving
y=cosx and its derivative
Same thing as above, but this time it becomes y=-sinx
Derivative of y=cosx is y=-sinx
Pattern: The cycle of derivatives with sinusoidal functions
f(x) = sinx
f’(x) = cosx
f’’(x) = -sinx
f’’’(x) = -cosx
f’’’’(x) = sinx
Pattern repeats over and over again
The rate of change of a sinusoidal function is periodic
The derivative of a sinusoidal function is a sinusoidal function
Degrees aren’t changing, it will forever remain a sinusoidal function
Finding the equation of a line that is tangent to a given function and passes through a point (or has a given x value as well)
Find derivative
Use special triangles (as we’re working with sin and cos)
Sub the x value into derivative and operate on it to find the slope
Use y=mx+b to find b (sub in (x,y) that is given; if it’s not given and you just have the x value, then sub into original equation to get the y coordinate so you have a full coordinate point)
Find your final equation
Derivatives of the Sine and Cosine Functions and Differentiation Rules for Sinusoidal Functions
f(x) = sinx → f’(x) = cosx
f(x) = cosx → f’(x) = -sinx
The power, chain, and product differentiation rules also apply to sinusoidal functions
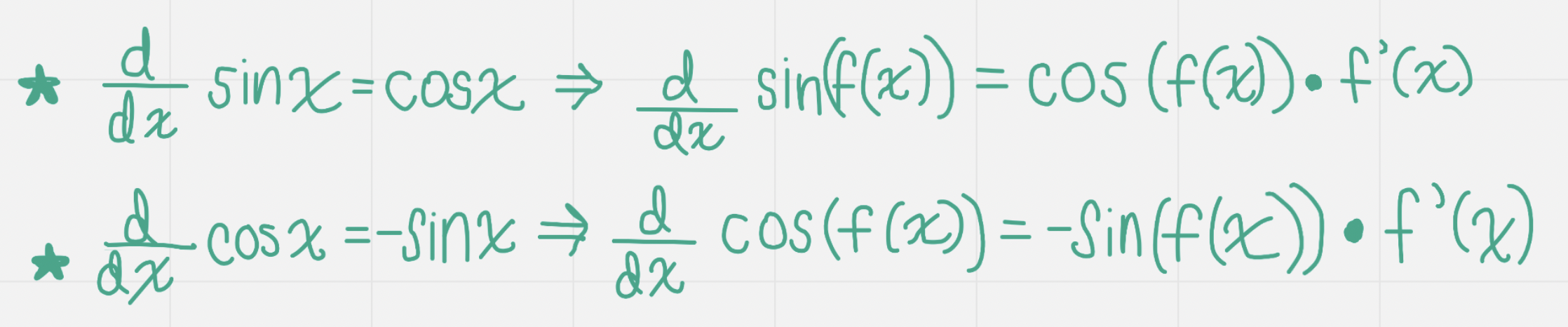
Review of Exponential and Logs
 Log functions are the inverse of exponential functions
Log functions are the inverse of exponential functions
 Log rules:
Log rules:
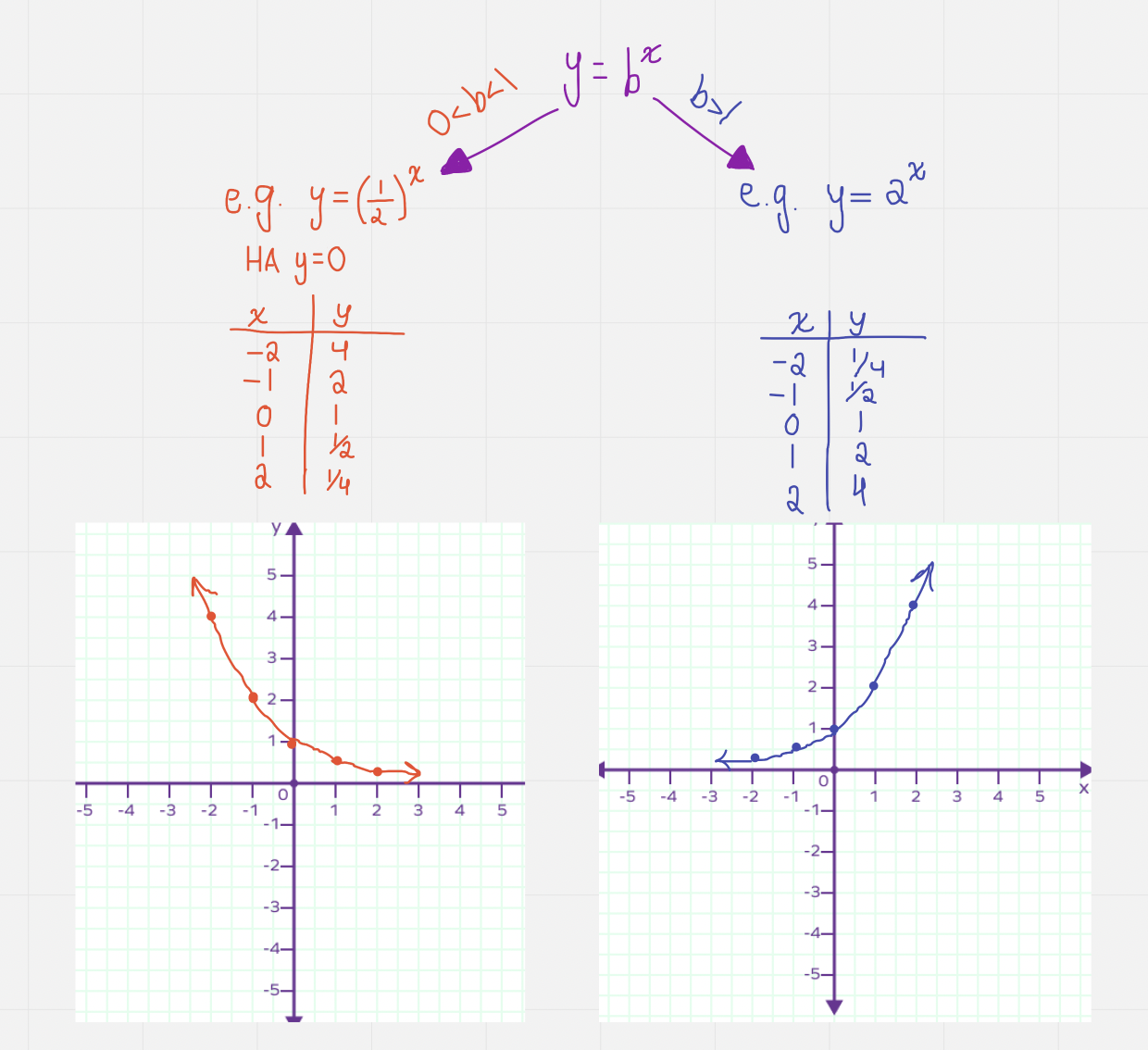
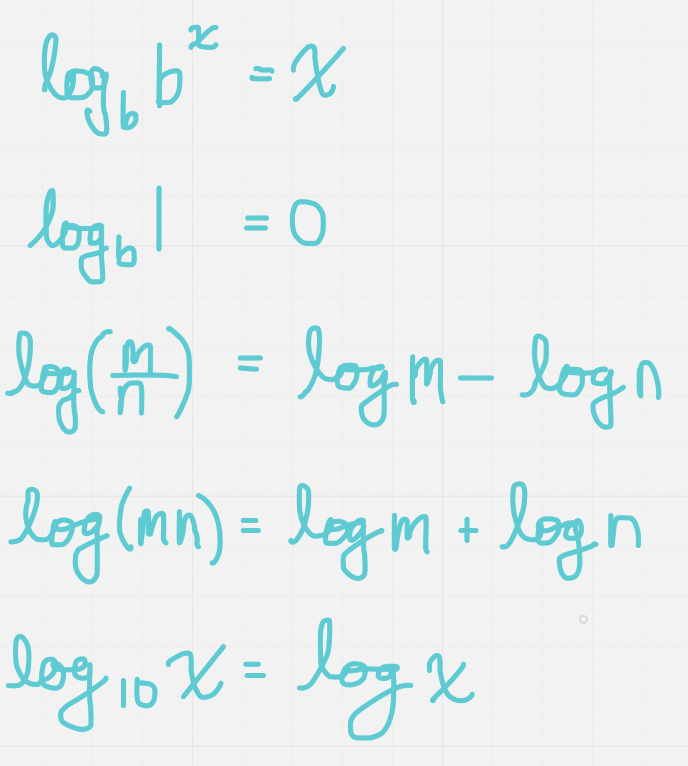 Exponential growth and decay
Exponential growth and decay
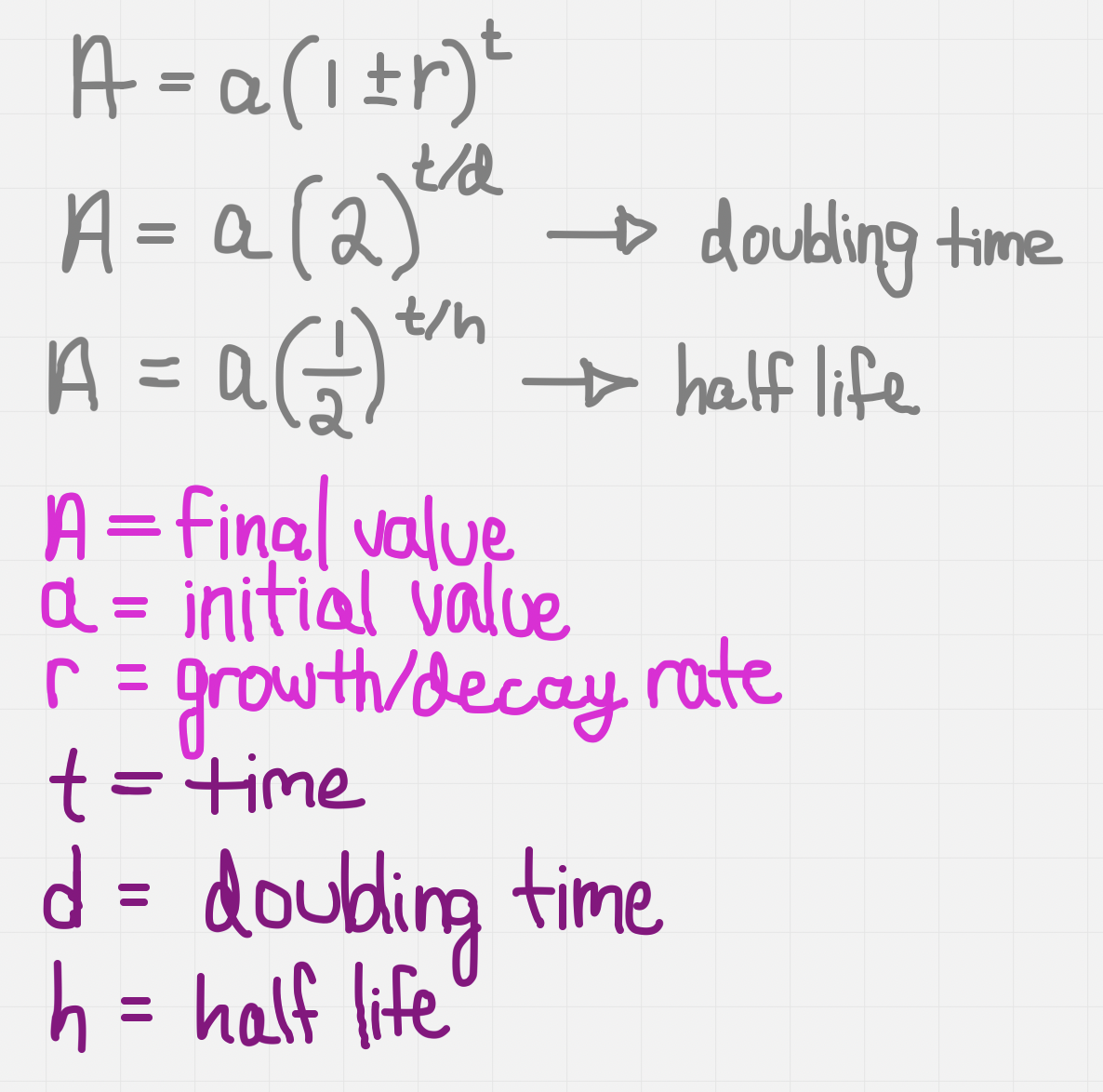 Rates of Change of Exponential Functions and the Number e
Rates of Change of Exponential Functions and the Number e
As x→∞ the IROC (slope of the tangent) is increasing
Rate of change is increasing exponentially, therefore the exponent of an exponential function is also an exponential function
Euler’s number e
Irrational number
Similar in nature to π
IROC for the natural exponential function f(x)=eˣ ⟹ f’(x)=eˣ
The derivative of an exponential function is an exponential function
e is known as Euler’s number is defined as a limit
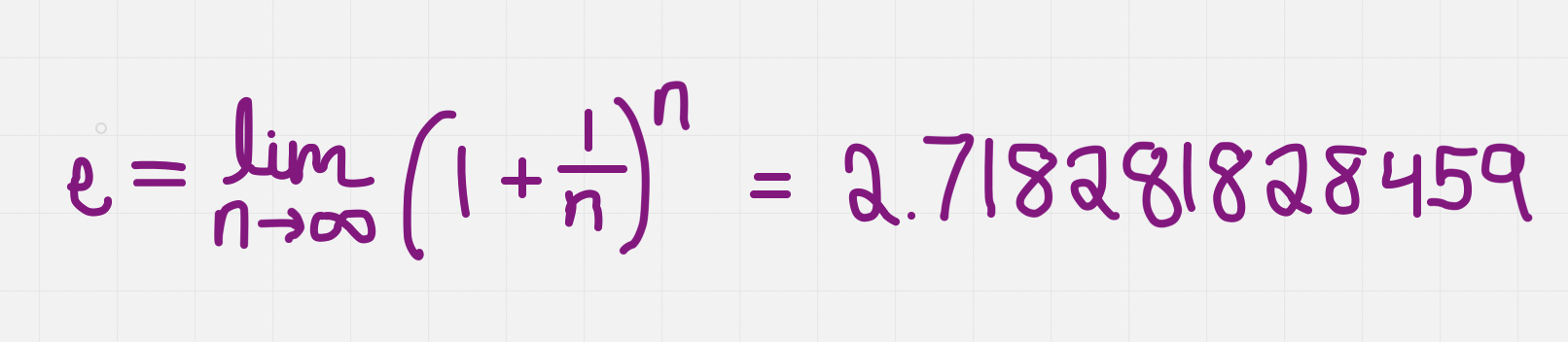
The natural log of x is defined as a log function with base e
ln has a log base e, a log with base of e
 Properties:
Properties:
 Important rules:
Important rules:
Derivatives of Exponential Functions
The derivative of an exponential function is an exponential function
If y=bˣ then y’ = kbˣ where k is some constant
Derivative of an exponential function:
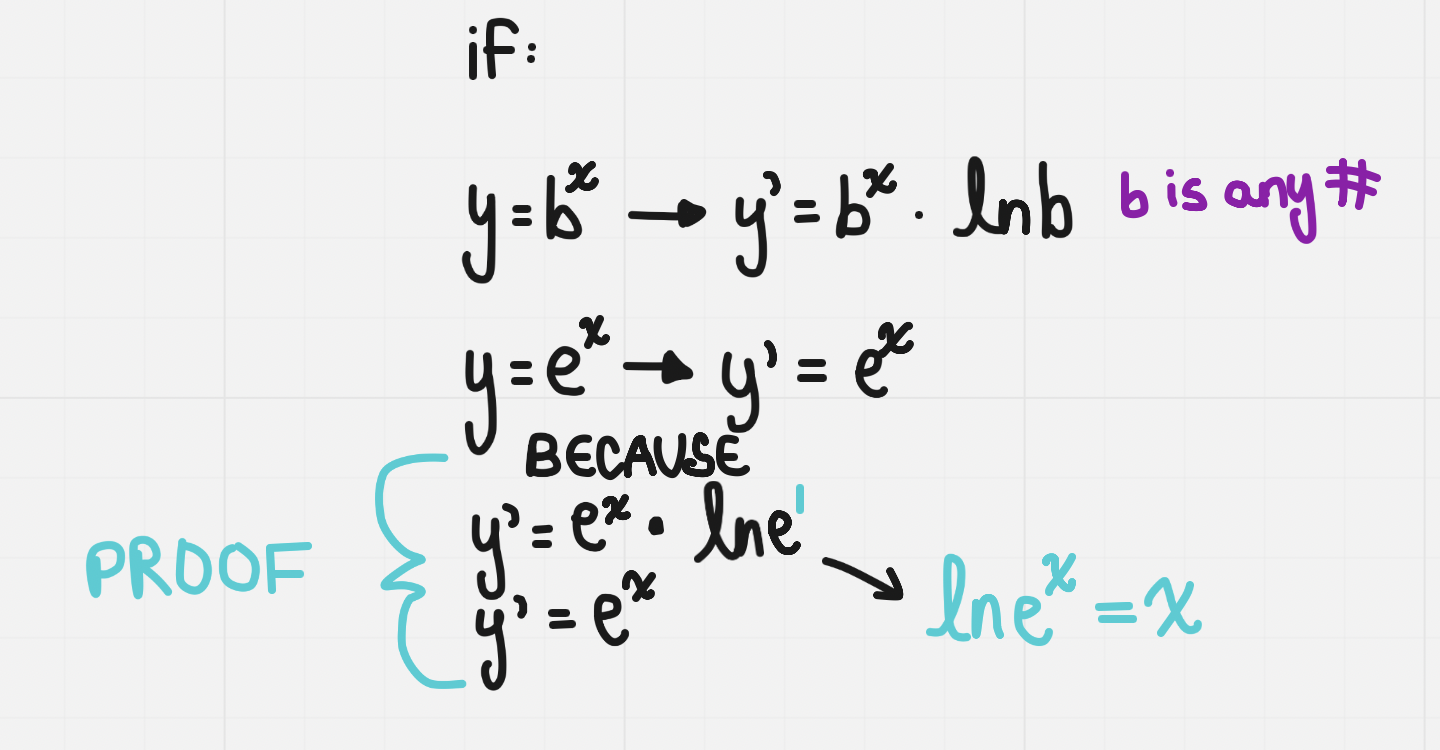
Differentiation Rules for Exponential Functions and Applications
Recall chain rule: h(x) = f’(g(x)) • g’(x)
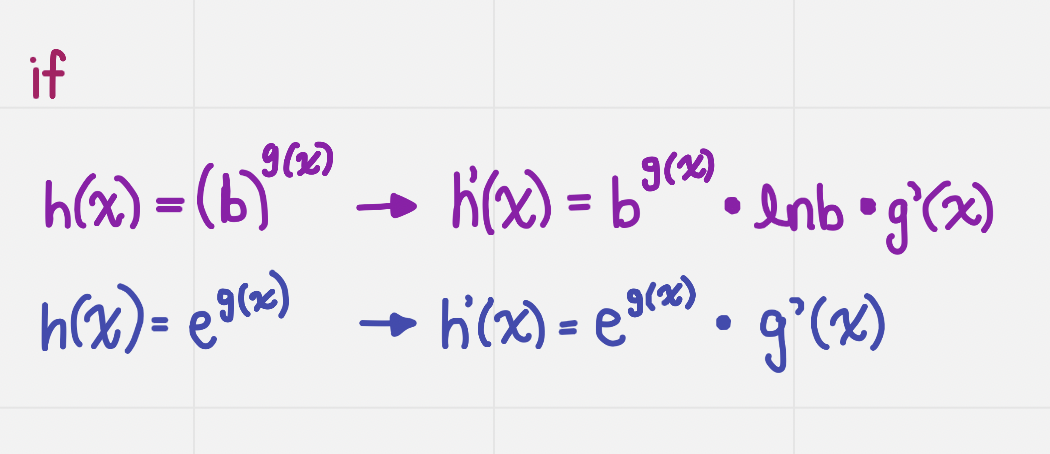
When word problems ask for “rate”: find the derivative
12-05: Special Derivatives (Sinusoidal and Exponential Functions)
IROC of Sinusoidal Functions
Sinusoidal function: functions where graphs have the same shape as a sine wave
Properties of sinusoidal functions:

y=sinx and its derivative
Derivative of y=sinx is y=cosx
This is because the slope of the tangent line gets “derivative-d” and then becomes a point
In the original, mtangent=1 when increasing, this becomes the new y value
→ Otherwise, consider the points where mtangent=0, these become intercepts as we learned before where min and max points become intercepts when deriving
y=cosx and its derivative
Same thing as above, but this time it becomes y=-sinx
Derivative of y=cosx is y=-sinx
Pattern: The cycle of derivatives with sinusoidal functions
f(x) = sinx
f’(x) = cosx
f’’(x) = -sinx
f’’’(x) = -cosx
f’’’’(x) = sinx
Pattern repeats over and over again
The rate of change of a sinusoidal function is periodic
The derivative of a sinusoidal function is a sinusoidal function
Degrees aren’t changing, it will forever remain a sinusoidal function
Finding the equation of a line that is tangent to a given function and passes through a point (or has a given x value as well)
Find derivative
Use special triangles (as we’re working with sin and cos)
Sub the x value into derivative and operate on it to find the slope
Use y=mx+b to find b (sub in (x,y) that is given; if it’s not given and you just have the x value, then sub into original equation to get the y coordinate so you have a full coordinate point)
Find your final equation
Derivatives of the Sine and Cosine Functions and Differentiation Rules for Sinusoidal Functions
f(x) = sinx → f’(x) = cosx
f(x) = cosx → f’(x) = -sinx
The power, chain, and product differentiation rules also apply to sinusoidal functions
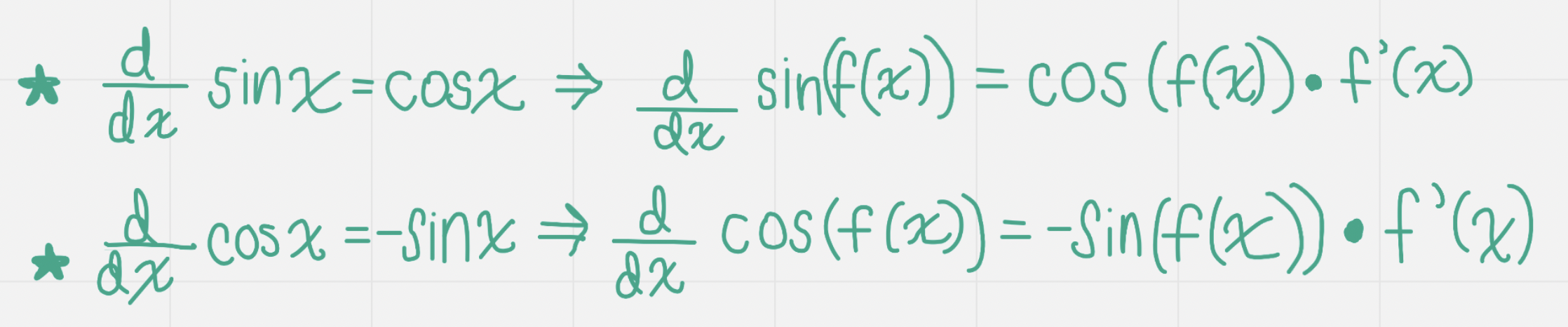
Review of Exponential and Logs
 Log functions are the inverse of exponential functions
Log functions are the inverse of exponential functions
 Log rules:
Log rules:
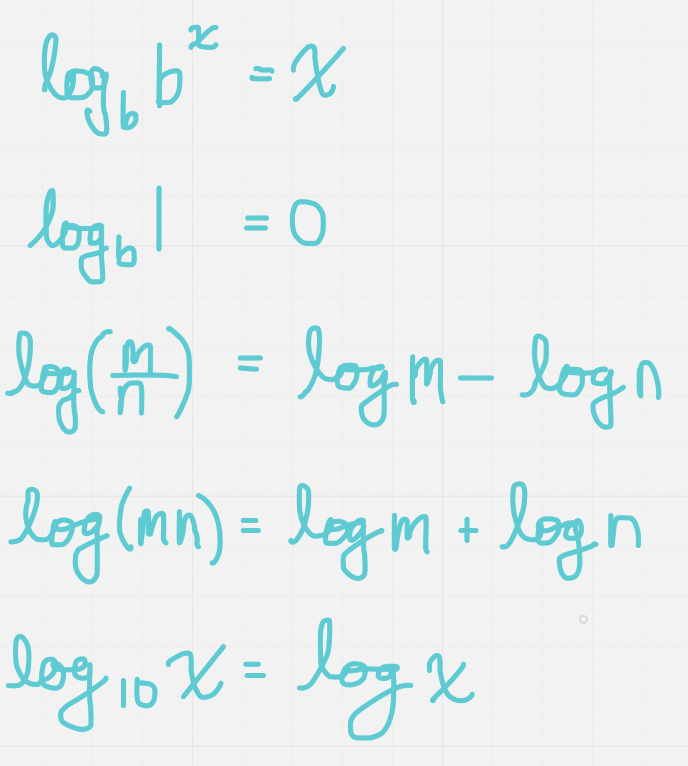 Exponential growth and decay
Exponential growth and decay
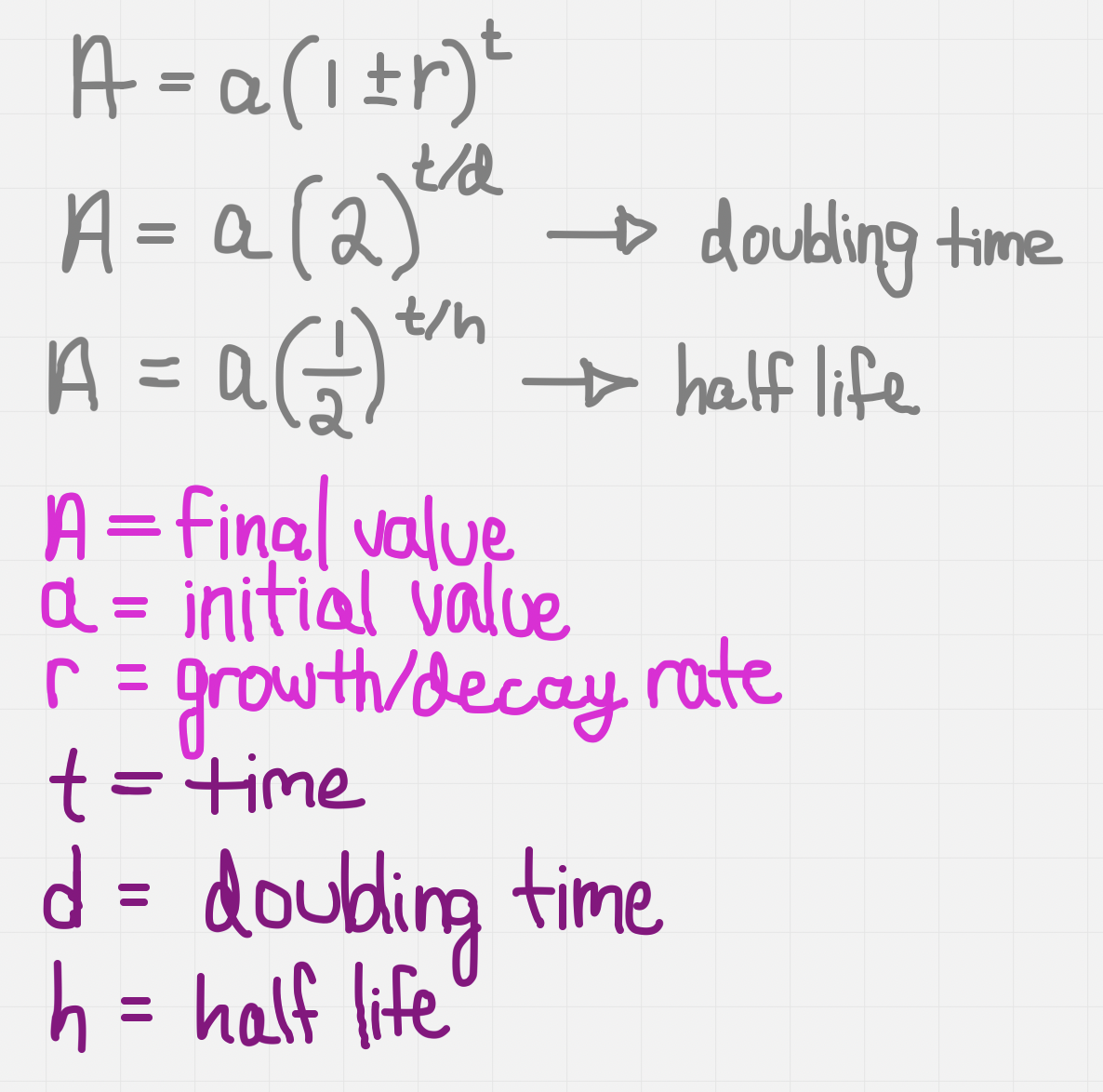 Rates of Change of Exponential Functions and the Number e
Rates of Change of Exponential Functions and the Number e
As x→∞ the IROC (slope of the tangent) is increasing
Rate of change is increasing exponentially, therefore the exponent of an exponential function is also an exponential function
Euler’s number e
Irrational number
Similar in nature to π
IROC for the natural exponential function f(x)=eˣ ⟹ f’(x)=eˣ
The derivative of an exponential function is an exponential function
e is known as Euler’s number is defined as a limit
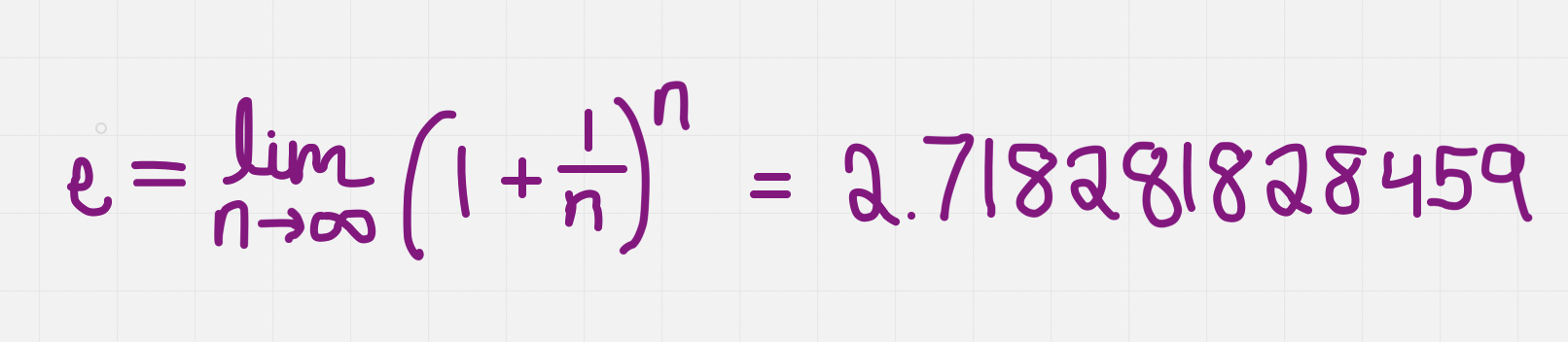
The natural log of x is defined as a log function with base e
ln has a log base e, a log with base of e
 Properties:
Properties:
 Important rules:
Important rules:
Derivatives of Exponential Functions
The derivative of an exponential function is an exponential function
If y=bˣ then y’ = kbˣ where k is some constant
Derivative of an exponential function:
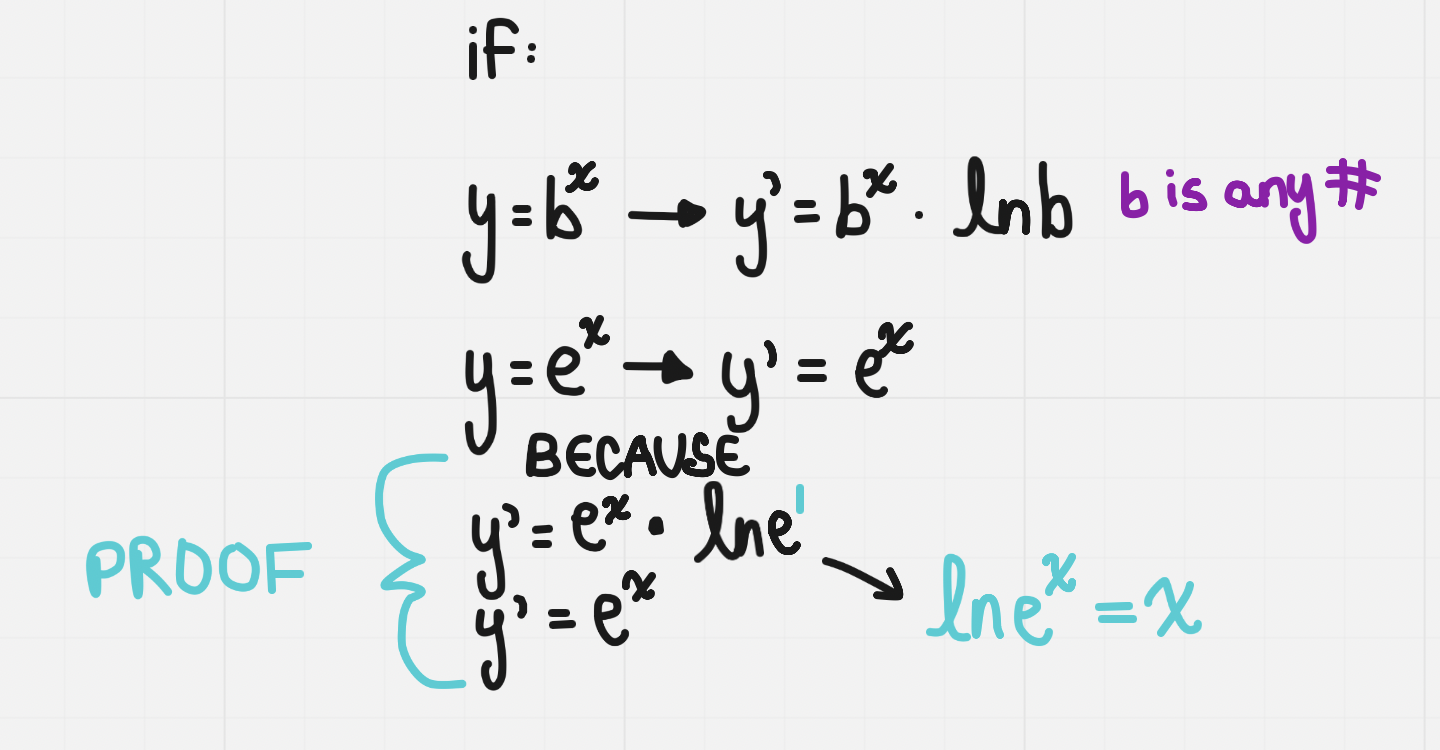
Differentiation Rules for Exponential Functions and Applications
Recall chain rule: h(x) = f’(g(x)) • g’(x)
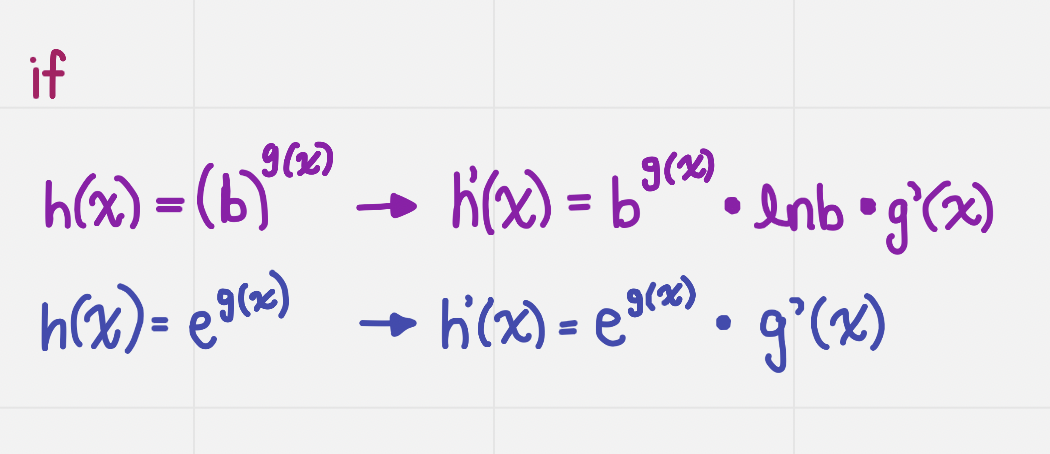
When word problems ask for “rate”: find the derivative
 Knowt
Knowt